What is DDM?
DDM, first developed by Cerbino and Trappe [Phys. Rev. Lett., 2008, 100, 188102], is an image analysis method that extracts statistical information about intensity fluctuation correlations from video microscopy images. In essence, it allows users to extract both qualitative and quantitative information about the important dynamical processes occuring within a video/material, including the important time and length scales associated with them. The correlation functions provided by DDM are analogous to quantities that are measured by other dynamic scattering and correlation spectroscopy methods (DLS, XPCS, etc.), and can be used to gain deep insight into dynamic and kinetic processes in complex fluids, biofluids and soft matter. Examples include:
- Accurate sizing of nanoparticles and colloidal objects (even when those objects are not clearly visible in an image).
- Quantifying rates associated with nucleation, growth and coarsening processes in phase separating materials.
- Analyzing swimming and collective motion of microorganisms and active fluids.
- Dynamics of concentrated suspensions, glasses and gels.
Why use DDM?
DDM analysis can be applied to video images acquired from conventional imaging modes including bright-field, DIC microscopy, confocal, fluorescence, and dark-field imaging. Because it collects high-fidelity statistics from conventional video images, it combines a number of the advantages of both imaging and scattering methods, while avoiding many of the challenges and drawbacks. Specifically, DDM:
- Can characterize spatially or dynamically heterogeneous materials.
- Can be applied to low signal-to-noise or optically dense samples.
- Requires small sample volumes.
- Requires no image-specific or user-defined empirical parameters (cutoff sizes, intensity scales, etc.).
- Uses unmodified microscopes and imaging systems.
How does DDM work?
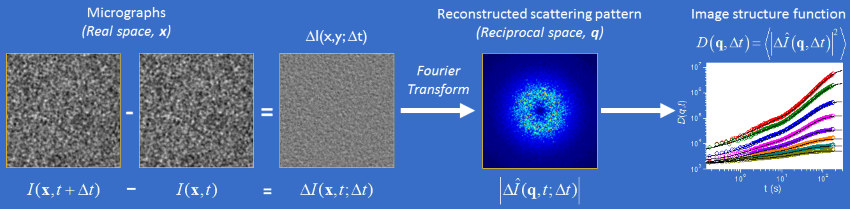
The DDM algorithm is graphically described above. The analysis is applied to a series of video images taken at a constant acquisition rate (frame rate), where each image can be described as a 2D greyscale intensity map, I(x,y,t). First, the algorithm locates all image pairs separated by a particular observation time, Δt. For each of these image pairs, a difference image, ΔI(x,y,Δt), is created by subtracting, pixel-by-pixel, one image from the other. Then, the algorithm computes the spatial Fourier transform (FFT) of each difference image, providing a 2D Fourier map of intensity fluctuation correlations, I(qx,qy,Δt), for that particular image pair. If one assumes that dynamical processes occuring in the image over the course of the video are not evolving with time, then I(qx,qy,Δt) can be averaged over all image pairs for a particular Δt, yielding the ensemble average 2D Fourier map, ⟨I(qx,qy,Δt)⟩. Finally, the "image structure function", D(qx,qy,Δt), is obtained by calculating the power spectrum of the average 2D Fourier map, D(qx,qy,Δt) = ⟨|I2(qx,qy,Δt)|⟩. The entire process is then repeated for all possible values of Δt in the image series.
DDMCalc - Perform DDM analysis in Matlab
As a resource for the soft matter research community, we have developed DDMCalc - a Matlab computer code and associated documentation for performing DDM analysis on video images. The code also includes a module for fitting DDM data to a model for discrete objects undergoing diffusive motion (e.g. Brownian particles). Further details about the code and associated computational methods can be found in a recent publication.
The DDMCalc software package includes Matlab codes, installation instructions, detailed documentation, and a brief tutorial (including sample data). DDMCalc is made freely available for download and use by non-commercial entities at the link below. The software was developed with support from the National Science Foundation under Award No. CBET 1351371.